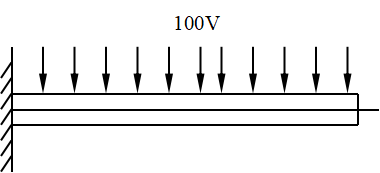导电聚合物的电-力、化-力耦合理论及数值计算
导电聚合物材料的电-力、化-力耦合理论和数值计算,利用电学、力学和化学势的基本方程推导出电-力耦合方程、化-力耦合方程,并且分别推导成等效积分弱形式,利用FEPG有限元编程,分别计算了电-力耦合、化-力耦合性能。研究表明,导电聚合物材料展现出明显的多场耦合效应,电场和化学势的作用导致聚合物材料的显著变形。
1、引 言
导电聚合物是经过掺杂和电化学过程使聚合物具有像金属一样的导电性能[1]。导电聚合物可分成湿的和干的两类。干的聚合物包括电致伸缩、静电、压电和铁电聚合物。他们一般要求比较高的驱动电压(>100 V/um)。但是,他们可以用直流电压诱发位移,这样可以提高使用的可靠性。另外,这些材料具有比较大的机械能密度。相反,湿的聚合物(离子交换,聚合物胶等)要求的驱动电压仅有1-2 Volts。但是,必须保持其是湿的状态,并且很难用直流电压诱发位移。干和湿导电聚合物产生的位移都可以是弯曲或者伸缩。
导电聚合物具有p-共轭分子链结构,在细观结构上是一种多相材料,其导电率取决于链结构和链间载流子(电子或离子)的传导性能。导电聚合物的结构和导电机理是,导电聚合物链上存在一些结构缺陷,孤电子没有参与共轭,通过氧化可以去掉它,形成碳正离子。反之,通过还原,可使它与外来电子配对,产生碳负离子,这类共轭缺陷并不只局限于一个碳原子上,而是分布在很长的导电聚合物链段上。由许许多多这种微观链按照一定的规律结合在一起,就形成了宏观的导电聚合物。
导电聚合物材料表现出电-力、电-化学耦合的性能。目前的研究工作较多地集中于对导电聚合物性能的实验测试上。文献[2]通过实验测试了导电聚合物的微结构、力学和电学性能。文献[3]研究了导电聚合物的电-化-力学变形和电化学势,并分析了它们的PH值相关性。文献[4]测试了导电聚合物混合体的热-力学行为。文献[5]测试了导电聚合物复合材料的电学和力学性能。
在理论研究方面,文献[6]利用均匀化模型预测了导电聚合物和碳纳米管的电导率,因为分子链的取向和微结构的不均匀性会严重地影响材料的导电性。文献[7]利用热力学第二定律,提出了一个统一的连续体模型用以模拟承受电-热-力相互作用和势效应的短链聚合物的多场耦合行为,如果略去电和热效应以后,该模型退化到纯力学的非线性流变方程。事实上,电-热-力耦合行为表现在许多材料中,例如压电陶瓷材料[8-11]。但是,目前对聚合物材料的多场耦合性能的知识了解很少,数值模拟研究更少。
本文讨论导电聚合物的电-力、电-化学耦合方程,在此基础上编制有限元程序分别求解这些方程,得到了在不同条件下,电-力、化-力效应诱发的材料变形。
2、电-力耦合数值算例
根据上面的理论,利用FEPG进行有限元编程,利用程序计算一个典型的例题。
算例:一个悬臂梁,左端完全约束,梁的几何尺寸如下:梁长L=100mm,梁高为1mm,弹性模量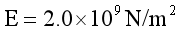 ,泊松比
,泊松比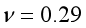 ,剪切模量
,剪切模量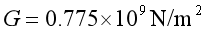 ,压电应力系数
,压电应力系数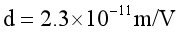 ,介电应力系数
,介电应力系数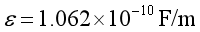 ,梁的上表面施加一个100V的电压,如下图1所示,求解梁中心线的变形。
,梁的上表面施加一个100V的电压,如下图1所示,求解梁中心线的变形。
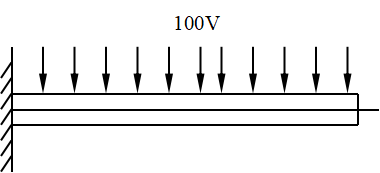 图1. 梁的电载荷示意图
在力-电耦合的有限元分析过程中,实际上弹性常数,电介质常数和压电常数存在不同的数量级,这将导致刚度矩阵严重的病态和不稳定的结果。利用上面的改变维数方法和FEPG有限元编程进行计算上面的算例,得到以下数值结果:
图1. 梁的电载荷示意图
在力-电耦合的有限元分析过程中,实际上弹性常数,电介质常数和压电常数存在不同的数量级,这将导致刚度矩阵严重的病态和不稳定的结果。利用上面的改变维数方法和FEPG有限元编程进行计算上面的算例,得到以下数值结果:
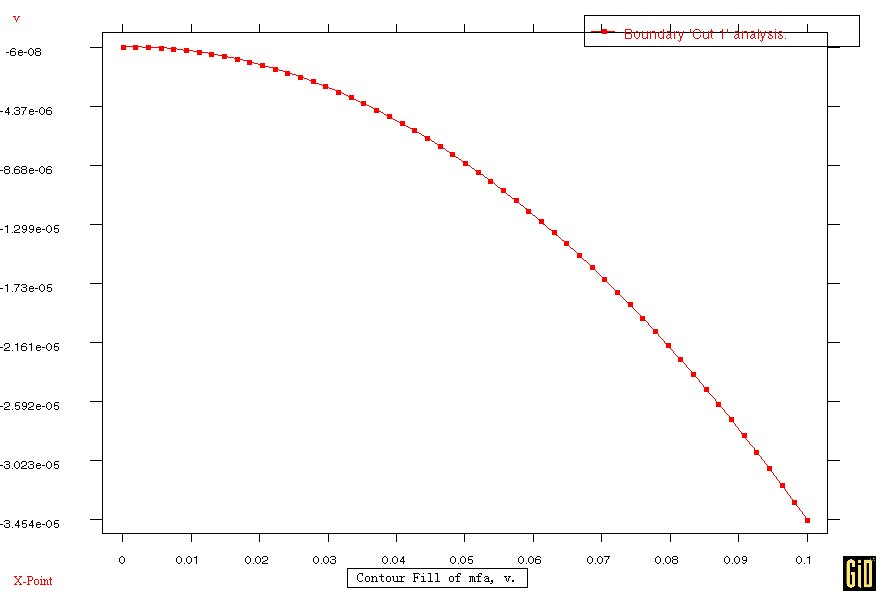 图2. 梁的变形图
针对本例题,利用ANSYS软件进行计算,并且与飞箭编程计算的结果进行比较,所得的结果如下:
图2. 梁的变形图
针对本例题,利用ANSYS软件进行计算,并且与飞箭编程计算的结果进行比较,所得的结果如下:
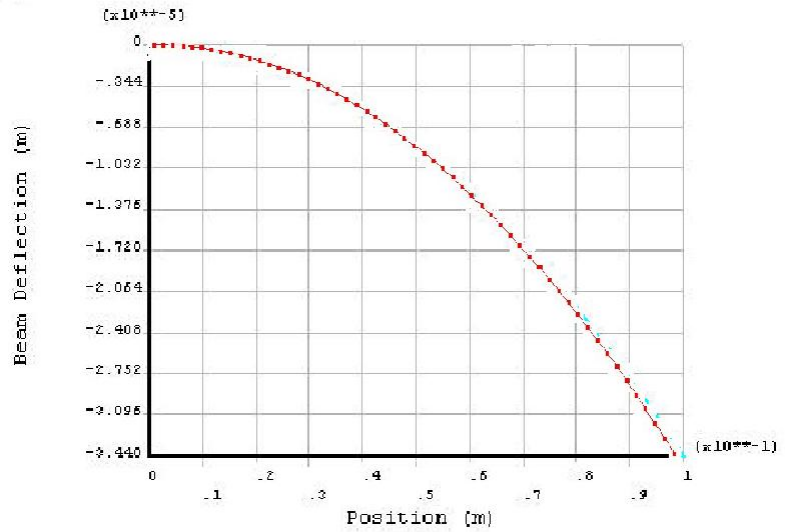 图3. 结果比较图
从上面算例的结果可以看出,利用fepg有限元编程求解结果与ANSYS软件求解结果比较吻合,也比较方便和准确的求解耦合问题。
图3. 结果比较图
从上面算例的结果可以看出,利用fepg有限元编程求解结果与ANSYS软件求解结果比较吻合,也比较方便和准确的求解耦合问题。
3、力-化学耦合数值算例
根据上面的理论,利用fepg软件进行有限元编程,利用程序计算一个典型的例题。
算例:一个平板,长L=100mm,宽为50mm,在板的中间施加一个100N和-100N的力,下边界施加一个完全的位移约束,浓度边界不施加约束,求该板由力产生的浓度分布。
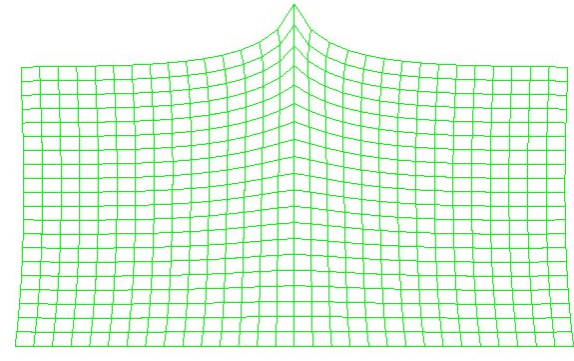
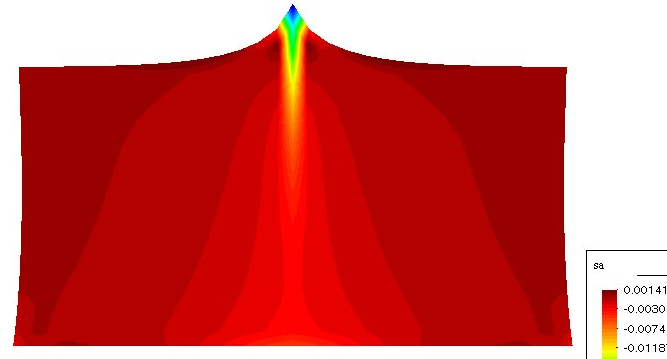 图4集中力100N载荷的浓度的分布图
图4集中力100N载荷的浓度的分布图
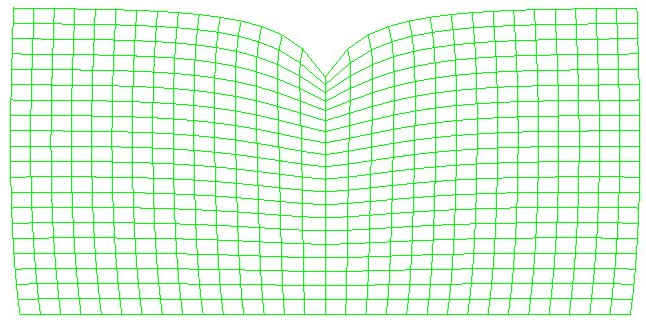
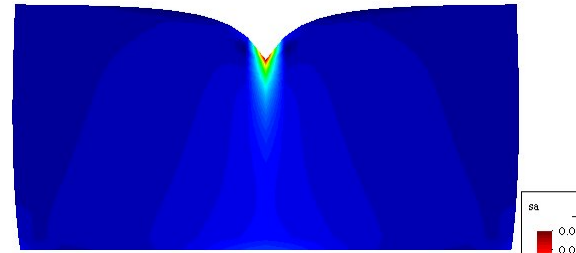 图4集中力-100N载荷的浓度的分布图
图4集中力-100N载荷的浓度的分布图
4、结论
本文分别讨论了导电聚合物电-力、力-化学耦合问题;根据力学,电学和化学的基本方程推导出耦合的等效积分弱形式;利用fepg软件进行编程求解耦合方程;模拟了导电聚合物多场耦合的特性。数值结果表明在耦合场作用下,导电聚合物具有电-力、力-化学耦合的特性,但是当各场的效应相差较大时,导电聚合物的性能受其中占优的场控制。在电-力场耦合作用下,导电聚合物的性能由环境变量控制,这种特性是导电聚合物用于传感器和致动器的主要因素。本文工作建立在线性材料模型的基础上,而参数对场变量的相关性将导致非线性模型,材料参数与计算结果的实验测试有待进一步研究。
参考文献
- Macdiarmid A. G., Synthetic metals: a novel role for organic polymers. Synthetic Metals, 2002, 125: 11-22
- Bhat N. V., Gader A. P., Bambole V. A., Structural, mechanical and electrical properties of electropolymerized polypyrrole composite films, Journal of Applied Polymer Science, 2001, 80: 2511-2517.
- Kanako M., Kaneto K., Electrochemomechanical deformation in polyaniline and poly (o-methoxyaniline), Synthetic Metals, 1999, 102:1350-1353.
- Gazotti Jr W. A., Faez R., De Paoli M-A., Thermal and mechanical behavior of a conductive elastomeric blend based on a soluble polyaniline derivative, European Polymer Journal, 1999, 35:35-40.
- Omastova M., Chodak I., Pionteck J., Electrical and mechanical properties of conducting polymer composites, Synthetic Metals, 1999, 102:1251-1252
- Kaiser A.B., Flanagan G. U., Stewart D. M., Beagehole D., Heterogeneous model for conduction in conducting polymers and carbon nanotubes, Synthetic Metals, 2001, 117:67-73.
- Eringen A. C., A unified continuum theory for electrodynamics of polymeric liquid crystals, International Journal of Engineering Science, 2000, 38:959-987.
- Benjeddou A. Advances in piezoelectric finite element modeling of adaptive structural elements: a survey. Computers and Structures, 2000, 76: 347-363.
- Qin Q H. Fracture Mechanics for Piezoelectric materials, WIT press, 2000.
- Tzou H S, Ye R. Piezothermoelasticity and precision control of piezoelectric system: theory and finite element analysis. J. Vibration and Acoustics. 1994, 116: 489-495.
- Lee H J, Saravanos D A. A mixed multi-field finite element formulation for thermopiezoelectric composite shells, Int. J. Solids and Structures, 2000, 37: 4949-4967.
- Hangqi, Daining Fang, Zhenhan Yao. FEM analysis of electro-mechanical coupling effect of piezoelectric materials, Computational Materials Science 8(1997)283-290.
- 有限元法在岩土力学中的应用。中国铁道出版社,1983。西德 G.哥德赫 编 张清、张弥译
- 石志飞,黄淑萍,张梓茂。饱和多孔介质耦合系统的变分原理。应用数学和力学。1999,3(20):249-256.
- 张钟鼎,王维彬,变形多孔介质众多相流问题的数值方法。安徽建筑工业学院学报,2001,1(9):30-33.
- 李伟,马骏,安延云的“三维Biot固结有限元方程的加权余量法推导”。海洋技术,1999, 4(18):72-79。
- Lewis. R.W.. The finite element method in the deformation and consolidation of porous media. Wiley, 1987.
- Benjamin, L. , Fernando, M. F. Simoes.. Articular cartilage with intra- and extra-brillar waters: a chemo-mechanical model, Mechanics of Materials 2004, 36: 515–541.
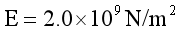 ,泊松比
,泊松比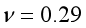 ,剪切模量
,剪切模量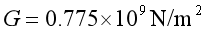 ,压电应力系数
,压电应力系数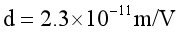 ,介电应力系数
,介电应力系数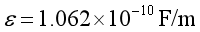 ,梁的上表面施加一个100V的电压,如下图1所示,求解梁中心线的变形。
,梁的上表面施加一个100V的电压,如下图1所示,求解梁中心线的变形。