导电材料的机电和化学机械耦合理论与数值计算
基于导电高分子材料的电-机械和化学-机械耦合理论和数值计算，利用电、机械和化学势的基本方程，推导了电-机械耦合方程和化学-机械耦合方程，并分别导出了等效积分的弱形式。利用FEPG有限元程序计算了电-机械耦合和化学-机械耦合性能。结果表明，导电高分子材料表现出明显的多场耦合效应，电场和化学势的作用导致高分子材料发生显著变形。
1.报价；word
导电聚合物通过掺杂和电化学过程与金属具有相同的导电性[1]。导电聚合物可分为湿聚合物和干聚合物。干聚合物包括电致伸缩、静电、压电和铁电聚合物。它们通常需要相对较高的驱动电压（>；100 V/um）。但是，他们可以使用直流电压来诱导位移，这可以提高使用的可靠性。此外，这些材料具有相对较大的机械能密度。相反，湿聚合物（离子交换、聚合物胶等）只需要1-2伏的驱动电压。然而，它必须保持湿润，并且很难用直流电压诱导位移。干湿导电聚合物产生的位移可以是弯曲或拉伸
导电聚合物具有p-共轭分子链结构。它是一种细观结构的非均匀材料。其导电性取决于链结构和链间载体（电子或离子）的导电性。导电聚合物的结构和导电机理是导电聚合物链中存在一些结构缺陷，孤电子不参与共轭。它可以通过氧化去除，形成碳正离子。相反，通过还原，它可以与外来电子配对，产生碳负离子。这种共轭缺陷并不局限于一个碳原子，而是分布在长的导电聚合物链段上。许多这些微链根据一定的规律结合形成宏观导电聚合物
导电聚合物材料具有电-机械和电化学耦合特性。目前，研究工作主要集中在导电聚合物性能的实验测试上。文献[2]测试了导电聚合物的微观结构、机械和电气性能。文献[3]研究了导电聚合物的电化学机械变形和电化学电位，并分析了它们的pH相关性。参考文献[4]测试了导电聚合物混合物的热机械行为。参考文献[5]对导电聚合物复合材料的电气和机械性能进行了测试。在理论研究方面，文献[6]使用均匀化模型预测导电聚合物和碳纳米管的导电性，因为分子链的取向和微观结构的不均匀性会严重影响材料的导电性。文献[7]利用热力学第二定律，提出了一个统一的连续介质模型来模拟短链聚合物在电-热-机械相互作用和势效应下的多场耦合行为。如果忽略电效应和热效应，模型将退化为纯机械非线性流变方程。事实上，电热-机械耦合行为表现在许多材料中，例如压电陶瓷材料[8-11]。然而，对聚合物材料的多场耦合特性的研究较少，数值模拟研究也较少。本文讨论了导电聚合物的机电耦合方程和电化学耦合方程。在此基础上，编制了有限元程序分别求解这些方程，得到了不同条件下由机电效应和化学机械效应引起的材料变形。
2.机电耦合的数值例子
，FEPG用于有限元编程，并使用该程序计算了一个典型示例
计算示例：悬臂梁在左端完全约束。梁的几何尺寸如下：梁长L=100mm，梁高1mm，弹性模量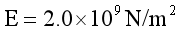
，泊松比
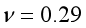，剪切模量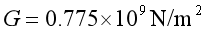
，压电应力系数
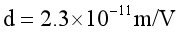，介电应力系数
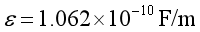。向梁的上表面施加100V电压，如下图1所示，以解决梁中心线的变形问题nbsp； ； ； ； ； ； ； ； ； ； ；图1.梁电载荷示意图在机电耦合有限元分析过程中，实际上弹性常数、介电常数和压电常数有不同的数量级，这将导致刚度矩阵产生严重的病态和不稳定的结果。采用上述变尺寸法和FEPG有限元程序对上述算例进行计算，得到以下数值结果：
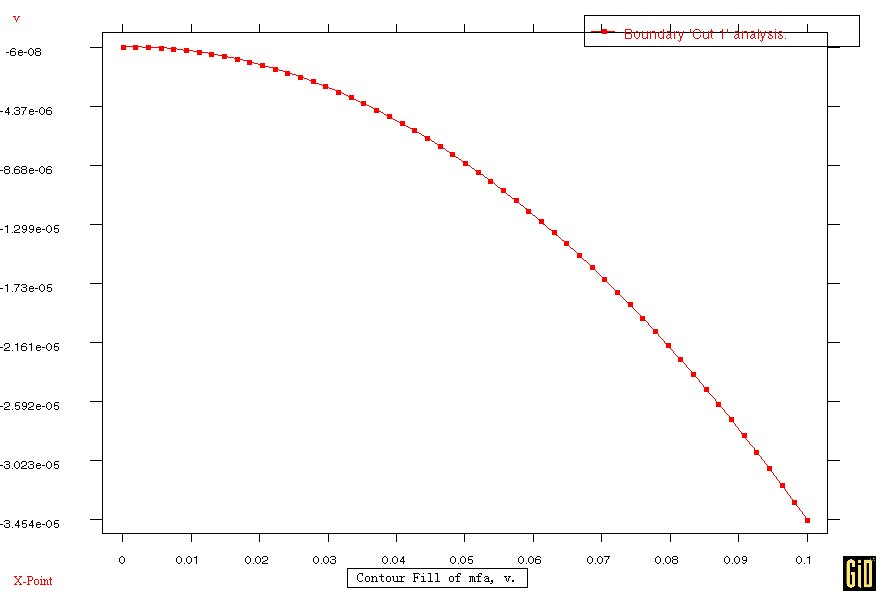
； ； ； ； ； ； ； ； ； ； ； ； ； ； ；图2.梁变形图
本例采用ANSYS软件进行计算，并与飞箭编程计算结果进行比较。结果如下：
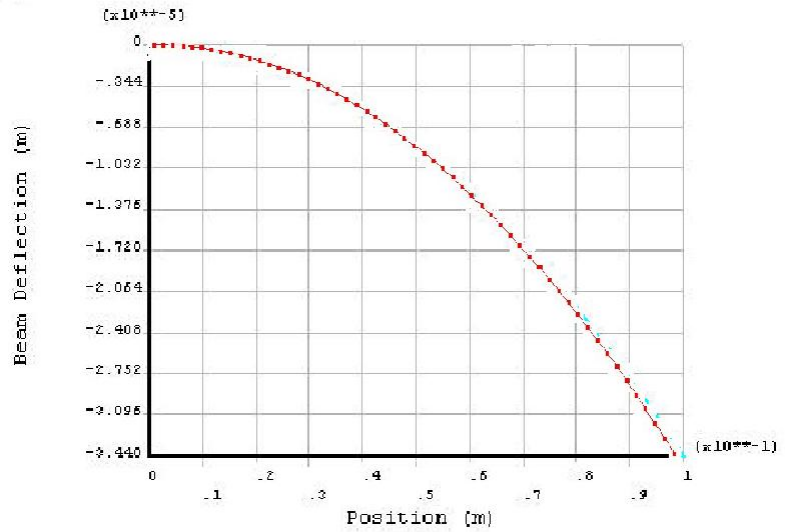
； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ；图3.结果对比从上述示例的结果可以看出，FEPG有限元编程的解算结果与ANSYS软件的解算结果一致，根据上述理论，利用FEPG软件进行了有限元程序设计，并用程序
计算实例：对于长度为L＝100mm、宽度为50mm的平板，在板中部施加100N和-100N的力，在下边界上施加完整的位移约束，在浓度边界上不施加约束。计算力
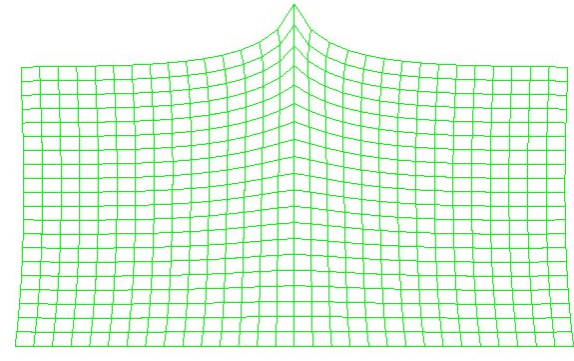
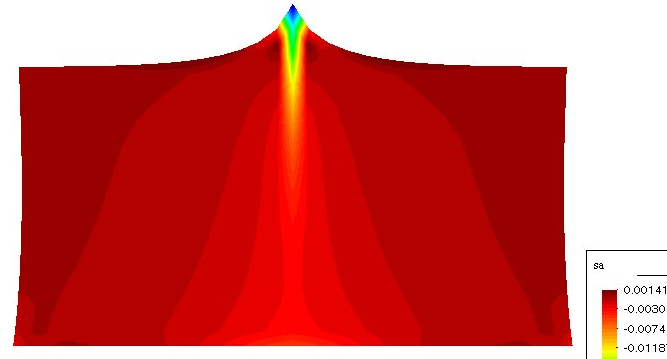
产生的板的浓度分布nbsp； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ；图4集中力100N荷载的集中分布
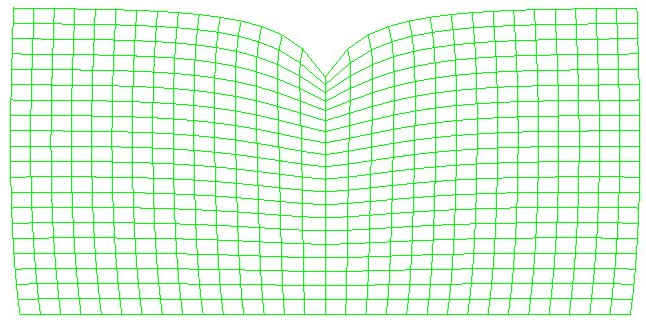{[111]}
nbsp； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ；图4集中力-100n载荷的浓度分布
结论
本文分别讨论了导电聚合物的机电耦合和机械力化学耦合问题；从力学、电学和化学的基本方程出发，导出了耦合的等效积分弱形式；用FEPG软件求解耦合方程；模拟了导电聚合物的多场耦合特性。数值计算结果表明，在耦合场作用下，导电聚合物具有电-机械和机械-化学耦合的特性，但当各场作用效果差异较大时，导电聚合物的性能受主导场的控制。在电场的耦合作用下，导电聚合物的性能受环境变量的控制，这是导电聚合物在传感器和执行器中应用的主要因素。本文的工作基于线性材料模型，参数与场变量的相关性将导致非线性模型。材料参数的实验测试和计算结果需要进一步研究
参考
Macdiarmid A。合成金属：有机聚合物的新角色。合成金属，2002，125:11-22。V.，Gader A。P.，班波尔五世。A.，电聚合聚吡咯复合膜的结构、机械和电气性能，应用聚合物科学杂志，2001，80:2511-2517。
Kanako M.，Kaneto K.，聚苯胺和聚邻甲氧基苯胺的电化学机械变形，合成金属，1999，102:1350-1353。
。A.，Faez R.，De Paoli M-A.，基于可溶性聚苯胺衍生物的导电弹性体混合物的热和机械行为，欧洲聚合物杂志，1999，35:35-40。
Omastova M.，Chodak I.，Pionteck J.，导电聚合物复合材料的电气和机械性能，合成金属，1999，102:1251-1252
Kaiser A.B。，弗拉纳根G。美国，斯图尔特。M.，Beagehole D.，导电聚合物和碳纳米管中传导的非均相模型，合成金属，2001，117:67-73。
Eringen A。C.，聚合物液晶电动力学的统一连续介质理论，国际工程科学杂志，2000年，38:959-987。
Benjeddou A。自适应结构元件的压电有限元建模进展：综述。计算机与结构，2000，76:347-363.
秦Q H。压电材料的断裂力学，威特出版社，2000。压电热弹性与压电系统的精密控制：理论与有限元分析。J振动与声学。1994年，116:489-495.
李H J，萨拉瓦诺斯D A。热压电复合材料壳体的混合多场有限元公式，Int.J。固体与结构，2000，37:4949-4967。
杭琦，方大宁，姚振汉。压电材料机电耦合效应的有限元分析，计算材料科学8（1997）283-290.
有限元法在岩土力学中的应用。中国铁路出版社，1983年，G。西德戈德赫；张青、张密译史志飞、黄淑萍、张子茂。饱和多孔介质耦合系统的变分原理。应用数学和力学。1999,3（20）：249-256.
张忠定，王伟斌，变形多孔介质中许多相流问题的数值方法。安徽建筑技术学院学报，2001，1（9）：30-33
李伟，马军，安彦云的&ldquo；用加权残数法推导三维Biot固结有限元方程&rdquo；。海洋技术，1999，4（18）：72-79.
刘易斯。多孔介质变形和固结的有限元方法。威利，1987。
本杰明，L，费尔南多，M。F西蒙斯。。具有纤颤内和纤颤外水的关节软骨：化学力学模型，材料力学2004，36:515&ndash；541名
；
导电聚合物通过掺杂和电化学过程与金属具有相同的导电性[1]。导电聚合物可分为湿聚合物和干聚合物。干聚合物包括电致伸缩、静电、压电和铁电聚合物。它们通常需要相对较高的驱动电压（>；100 V/um）。但是，他们可以使用直流电压来诱导位移，这可以提高使用的可靠性。此外，这些材料具有相对较大的机械能密度。相反，湿聚合物（离子交换、聚合物胶等）只需要1-2伏的驱动电压。然而，它必须保持湿润，并且很难用直流电压诱导位移。干湿导电聚合物产生的位移可以是弯曲或拉伸
导电聚合物具有p-共轭分子链结构。它是一种细观结构的非均匀材料。其导电性取决于链结构和链间载体（电子或离子）的导电性。导电聚合物的结构和导电机理是导电聚合物链中存在一些结构缺陷，孤电子不参与共轭。它可以通过氧化去除，形成碳正离子。相反，通过还原，它可以与外来电子配对，产生碳负离子。这种共轭缺陷并不局限于一个碳原子，而是分布在长的导电聚合物链段上。许多这些微链根据一定的规律结合形成宏观导电聚合物
导电聚合物材料具有电-机械和电化学耦合特性。目前，研究工作主要集中在导电聚合物性能的实验测试上。文献[2]测试了导电聚合物的微观结构、机械和电气性能。文献[3]研究了导电聚合物的电化学机械变形和电化学电位，并分析了它们的pH相关性。参考文献[4]测试了导电聚合物混合物的热机械行为。参考文献[5]对导电聚合物复合材料的电气和机械性能进行了测试。在理论研究方面，文献[6]使用均匀化模型预测导电聚合物和碳纳米管的导电性，因为分子链的取向和微观结构的不均匀性会严重影响材料的导电性。文献[7]利用热力学第二定律，提出了一个统一的连续介质模型来模拟短链聚合物在电-热-机械相互作用和势效应下的多场耦合行为。如果忽略电效应和热效应，模型将退化为纯机械非线性流变方程。事实上，电热-机械耦合行为表现在许多材料中，例如压电陶瓷材料[8-11]。然而，对聚合物材料的多场耦合特性的研究较少，数值模拟研究也较少。本文讨论了导电聚合物的机电耦合方程和电化学耦合方程。在此基础上，编制了有限元程序分别求解这些方程，得到了不同条件下由机电效应和化学机械效应引起的材料变形。
2.机电耦合的数值例子
，FEPG用于有限元编程，并使用该程序计算了一个典型示例
计算示例：悬臂梁在左端完全约束。梁的几何尺寸如下：梁长L=100mm，梁高1mm，弹性模量
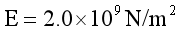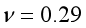，泊松比，剪切模量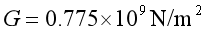，压电应力系数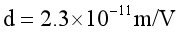，介电应力系数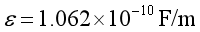。向梁的上表面施加100V电压，如下图1所示，以解决梁中心线的变形问题nbsp； ； ； ； ； ； ； ； ； ； ；图1.梁电载荷示意图在机电耦合有限元分析过程中，实际上弹性常数、介电常数和压电常数有不同的数量级，这将导致刚度矩阵产生严重的病态和不稳定的结果。采用上述变尺寸法和FEPG有限元程序对上述算例进行计算，得到以下数值结果：； ； ； ； ； ； ； ； ； ； ； ； ； ； ；图2.梁变形图
本例采用ANSYS软件进行计算，并与飞箭编程计算结果进行比较。结果如下：
； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ；图3.结果对比从上述示例的结果可以看出，FEPG有限元编程的解算结果与ANSYS软件的解算结果一致，根据上述理论，利用FEPG软件进行了有限元程序设计，并用程序
计算实例：对于长度为L＝100mm、宽度为50mm的平板，在板中部施加100N和-100N的力，在下边界上施加完整的位移约束，在浓度边界上不施加约束。计算力
产生的板的浓度分布nbsp； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ；图4集中力100N荷载的集中分布
{[111]}nbsp； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ； ；图4集中力-100n载荷的浓度分布
结论
本文分别讨论了导电聚合物的机电耦合和机械力化学耦合问题；从力学、电学和化学的基本方程出发，导出了耦合的等效积分弱形式；用FEPG软件求解耦合方程；模拟了导电聚合物的多场耦合特性。数值计算结果表明，在耦合场作用下，导电聚合物具有电-机械和机械-化学耦合的特性，但当各场作用效果差异较大时，导电聚合物的性能受主导场的控制。在电场的耦合作用下，导电聚合物的性能受环境变量的控制，这是导电聚合物在传感器和执行器中应用的主要因素。本文的工作基于线性材料模型，参数与场变量的相关性将导致非线性模型。材料参数的实验测试和计算结果需要进一步研究
参考
Macdiarmid A。合成金属：有机聚合物的新角色。合成金属，2002，125:11-22。V.，Gader A。P.，班波尔五世。A.，电聚合聚吡咯复合膜的结构、机械和电气性能，应用聚合物科学杂志，2001，80:2511-2517。
Kanako M.，Kaneto K.，聚苯胺和聚邻甲氧基苯胺的电化学机械变形，合成金属，1999，102:1350-1353。
。A.，Faez R.，De Paoli M-A.，基于可溶性聚苯胺衍生物的导电弹性体混合物的热和机械行为，欧洲聚合物杂志，1999，35:35-40。
Omastova M.，Chodak I.，Pionteck J.，导电聚合物复合材料的电气和机械性能，合成金属，1999，102:1251-1252
Kaiser A.B。，弗拉纳根G。美国，斯图尔特。M.，Beagehole D.，导电聚合物和碳纳米管中传导的非均相模型，合成金属，2001，117:67-73。
Eringen A。C.，聚合物液晶电动力学的统一连续介质理论，国际工程科学杂志，2000年，38:959-987。
Benjeddou A。自适应结构元件的压电有限元建模进展：综述。计算机与结构，2000，76:347-363.
秦Q H。压电材料的断裂力学，威特出版社，2000。压电热弹性与压电系统的精密控制：理论与有限元分析。J振动与声学。1994年，116:489-495.
李H J，萨拉瓦诺斯D A。热压电复合材料壳体的混合多场有限元公式，Int.J。固体与结构，2000，37:4949-4967。
杭琦，方大宁，姚振汉。压电材料机电耦合效应的有限元分析，计算材料科学8（1997）283-290.
有限元法在岩土力学中的应用。中国铁路出版社，1983年，G。西德戈德赫；张青、张密译史志飞、黄淑萍、张子茂。饱和多孔介质耦合系统的变分原理。应用数学和力学。1999,3（20）：249-256.
张忠定，王伟斌，变形多孔介质中许多相流问题的数值方法。安徽建筑技术学院学报，2001，1（9）：30-33
李伟，马军，安彦云的&ldquo；用加权残数法推导三维Biot固结有限元方程&rdquo；。海洋技术，1999，4（18）：72-79.
刘易斯。多孔介质变形和固结的有限元方法。威利，1987。
本杰明，L，费尔南多，M。F西蒙斯。。具有纤颤内和纤颤外水的关节软骨：化学力学模型，材料力学2004，36:515&ndash；541名
；
